On Finding Areas by Integrating

One use of the integral calculus is to enable us to ascertain the values of areas bounded by curves.

Let us try to get at the subject bit by bit.

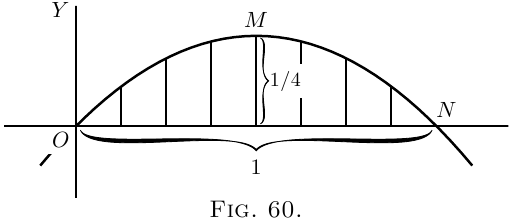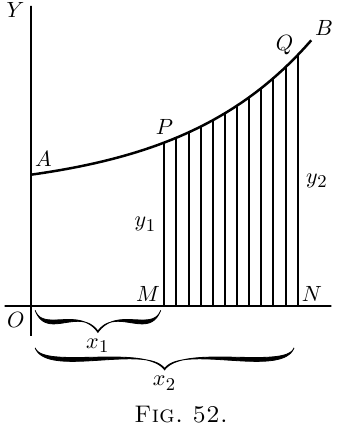
Let $AB$ (Figure 52) be a curve, the equation to which is known. That is, $y$ in this curve is some known function of $x$. Think of a piece of the curve from the point $P$ to the point $Q$.

Let a perpendicular $PM$ be dropped from $P$, and another $QN$ from the point $Q$. Then call $OM = x_1$ and $ON = x_2$, and the ordinates $PM = y_1$ and $QN = y_2$. We have thus marked out the area $PQNM$ that lies beneath the piece $PQ$. The problem is, how can we calculate the value of this area?

The secret of solving this problem is to conceive the area as being divided up into a lot of narrow strips, each of them being of the width $dx$. The smaller we take $dx$, the more of them there will be between $x_1$ and $x_2$. Now, the whole area is clearly equal to the sum of the areas of all such strips. Our business will then be to discover an expression for the area of any one narrow strip, and to integrate it so as to add together all the strips. Now think of any one of the strips. It will be like this: being bounded between two vertical sides, with a flat bottom $dx$, and with a slightly curved sloping top.

Suppose we take its average height as being $y$; then, as its width is $dx$, its area will be $y\, dx$. And seeing that we may take the width as narrow as we please, if we only take it narrow enough its average height will be the same as the height at the middle of it. Now let us call the unknown value of the whole area $S$, meaning surface. The area of one strip will be simply a bit of the whole area, and may therefore be called $dS$. So we may write \[ \text{area of $1$ strip} = dS = y · dx. \] If then we add up all the strips, we get \[ \text{total area $S$} = \int dS = \int y\, dx. \]

So then our finding $S$ depends on whether we can integrate $y · dx$ for the particular case, when we know what the value of $y$ is as a function of $x$.

For instance, if you were told that for the particular curve in question $y = b + ax^2$, no doubt you could put that value into the expression and say: then I must find $\int (b + ax^2)\, dx$.

That is all very well; but a little thought will show you that something more must be done. Because the area we are trying to find is not the area under the whole length of the curve, but only the area limited on the left by $PM$, and on the right by $QN$, it follows that we must do something to define our area between those "limits".

This introduces us to a new notion, namely that of integrating between limits. We suppose $x$ to vary, and for the present purpose we do not require any value of $x$ below $x_1$ (that is $OM$), nor any value of $x$ above $x_2$ (that is $ON$). When an integral is to be thus defined between two limits, we call the lower of the two values the inferior limit, and the upper value the superior limit. Any integral so limited we designate as a definite integral, by way of distinguishing it from a general integral to which no limits are assigned.

In the symbols which give instructions to integrate, the limits are marked by putting them at the top and bottom respectively of the sign of integration. Thus the instruction \[ \int_{x=x_1}^{x=x_2} y · dx \] will be read: find the integral of $y · dx$ between the inferior limit $x_1$ and the superior limit $x_2$.

Sometimes the thing is written more simply \[ \int^{x_2}_{x_1} y · dx. \] Well, but how do you find an integral between limits, when you have got these instructions?

Look again at Figure 52. Suppose we could find the area under the larger piece of curve from $A$ to $Q$, that is from $x = 0$ to $x = x_2$, naming the area $AQNO$. Then, suppose we could find the area under the smaller piece from $A$ to $P$, that is from $x = 0$ to $x = x_1$, namely the area $APMO$. If then we were to subtract the smaller area from the larger, we should have left as a remainder the area $PQNM$, which is what we want. Here we have the clue as to what to do; the definite integral between the two limits is the difference between the integral worked out for the superior limit and the integral worked out for the lower limit.

Let us then go ahead. First, find the general integral thus: \[ \int y\, dx, \] and, as $y = b + ax^2$ is the equation to the curve (Figure 52), \[ \int (b + ax^2)\, dx \] is the general integral which we must find.

Doing the integration in question by the rule , we get \[ bx + \frac{a}{3} x^3 + C; \] and this will be the whole area from $0$ up to any value of $x$ that we may assign.

Therefore, the larger area up to the superior limit $x_2$ will be \[ bx_2 + \frac{a}{3} x_2^3 + C; \] and the smaller area up to the inferior limit $x_1$ will be \[ bx_1 + \frac{a}{3} x_1^3 + C. \]

Now, subtract the smaller from the larger, and we get for the area $S$ the value, \[ \text{area $S$} = b(x_2 - x_1) + \frac{a}{3}(x_2^3 - x_1^3). \]

This is the answer we wanted. Let us give some numerical values. Suppose $b = 10$, $a = 0.06$, and $x_2 = 8$ and $x_1 = 6$. Then the area $S$ is equal to \begin{gather*} 10(8 - 6) + \frac{0.06}{3} (8^3 - 6^3) \\ \begin{aligned} &= 20 + 0.02(512 - 216) \\ &= 20 + 0.02 × 296 \\ &= 20 + 5.92 \\ &= 25.92. \end{aligned} \end{gather*}

Let us here put down a symbolic way of stating what we have ascertained about limits: \[ \int^{x=x_2}_{x=x_1} y\, dx = y_2 - y_1, \] where $y_2$ is the integrated value of $y\, dx$ corresponding to $x_2$, and $y_1$ that corresponding to $x_1$.

All integration between limits requires the difference between two values to be thus found. Also note that, in making the subtraction the added constant $C$ has disappeared.

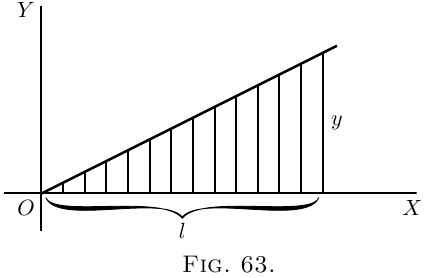
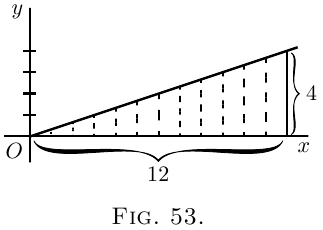
Examples (1) To familiarize ourselves with the process, let us take a case of which we know the answer beforehand. Let us find the area of the triangle (Figure 53), which has base $x = 12$ and height $y = 4$. We know beforehand, from obvious mensuration, that the answer will come $24$.

Now, here we have as the “curve” a sloping line for which the equation is \[ y = \frac{x}{3}. \]

The area in question will be \[ \int^{x=12}_{x=0} y · dx = \int^{x=12}_{x=0} \frac{x}{3} · dx. \]

Integrating $\dfrac{x}{3}\, dx$ (here), and putting down the value of the general integral in square brackets with the limits marked above and below, we get \begin{align*} \text{area}\; &= \left[ \frac{1}{3} · \frac{1}{2} x^2 \right]^{x=12}_{x=0} + C \\ &= \left[ \frac{x^2}{6} \right]^{x=12}_{x=0} + C \\ &= \left[ \frac{12^2}{6} \right] - \left[ \frac{0^2}{6} \right] \\ &= \frac{144}{6} = 24.\quad Ans. \end{align*}

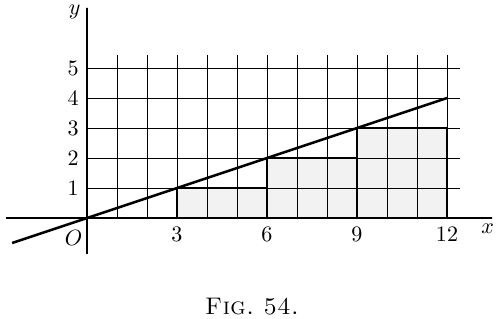
Let us satisfy ourselves about this rather surprising dodge of calculation, by testing it on a simple example. Get some squared paper, preferably some that is ruled in little squares of one-eighth inch or one-tenth inch each way. On this squared paper plot out the graph of the equation, \[ y = \frac{x}{3}. \]

The values to be plotted will be:

The plot is given in Figure 54.

Now reckon out the area beneath the curve by counting the little squares below the line, from $x = 0$ as far as $x = 12$ on the right. There are $18$ whole squares and four triangles, each of which has an area equal to $1\frac{1}{2}$ squares; or, in total, $24$ squares. Hence $24$ is the numerical value of the integral of $\dfrac{x}{3}\, dx$ between the lower limit of $x = 0$ and the higher limit of $x = 12$.

As a further exercise, show that the value of the same integral between the limits of $x = 3$ and $x = 15$ is $36$.

(2) Find the area, between limits $x = x_1$ and $x = 0$, of the curve $y = \dfrac{b}{x + a}$. \begin{align*} \text{Area} &= \int^{x=x_1}_{x=0} y · dx = \int^{x=x_1}_{x=0} \frac{b}{x+a}\, dx \\ &= b \bigl[\log_\epsilon(x + a) \bigr]^{x_1} _{0} + C \\ &= b \bigl[\log_\epsilon(x_1 + a) - \log_\epsilon(0 + a)\bigr] \\ &= b \log_\epsilon \frac{x_1 + a}{a}.\quad Ans . \end{align*}

Note–Notice that in dealing with definite integrals the constant $C$ always disappears by subtraction.

Let it be noted that this process of subtracting one part from a larger to find the difference is really a common practice. How do you find the area of a plane ring (Figure 56), the outer radius of which is $r_2$ and the inner radius is $r_1$? You know from mensuration that the area of the outer circle is $\pi r_2^2$; then you find the area of the inner circle, $\pi r_1^2$; then you subtract the latter from the former, and find area of ring $= \pi(r_2^2 - r_1^2)$; which may be written \[ \pi(r_2 + r_1)(r_2 - r_1) \] $= \text{mean circumference of ring} × \text{width of ring}$.

(3) Here's another case–that of the die-away curve. Find the area between $x = 0$ and $x = a$, of the curve (Figure 57) whose equation is \begin{align*} y &= b\epsilon^{-x}. \\ \text{Area} &= b\int^{x=a} _{x=0} \epsilon^{-x} · dx. \\ \end{align*} The integration (here) gives \begin{align*} &= b\left[-\epsilon^{-x}\right]^a _0 \\ &= b\bigl[-\epsilon^{-a} - (-\epsilon^{-0})\bigr] \\ &= b(1-\epsilon^{-a}). \end{align*}

(4) Another example is afforded by the adiabatic curve of a perfect gas, the equation to which is $pv^n = c$, where $p$ stands for pressure, $v$ for volume, and $n$ is of the value $1.42$ (Figure 58).

Find the area under the curve (which is proportional to the work done in suddenly compressing the gas) from volume $v_2$ to volume $v_1$.

Here we have \begin{align*} \text{area} &= \int^{v=v_2}_{v=v_1} cv^{-n} · dv \\ &= c\left[\frac{1}{1-n} v^{1-n} \right]^{v_2} _{v_1} \\ &= c \frac{1}{1-n} (v_2^{1-n} - v_1^{1-n}) \\ &= \frac{-c}{0.42}\left(\frac{1}{v_2^{0.42}} - \frac{1}{v_1^{0.42}}\right). \end{align*}

An Exercise.

Prove the ordinary mensuration formula, that the area $A$ of a circle whose radius is $R$, is equal to $\pi R^2$.

Consider an elementary zone or annulus of the surface (Figure 59), of breadth $dr$, situated at a distance $r$ from the centre. We may consider the entire surface as consisting of such narrow zones, and the whole area $A$ will simply be the integral of all such elementary zones from centre to margin, that is, integrated from $r = 0$ to $r = R$.

We have therefore to find an expression for the elementary area $dA$ of the narrow zone. Think of it as a strip of breadth $dr$, and of a length that is the periphery of the circle of radius $r$, that is, a length of $2 \pi r$. Then we have, as the area of the narrow zone, \[ dA = 2 \pi r\, dr. \]

Hence the area of the whole circle will be: \[ A = \int dA = \int^{r=R}_{r=0} 2 \pi r · dr = 2 \pi \int^{r=R}_{r=0} r · dr. \]

Now, the general integral of $r · dr$ is $\frac{1}{2} r^2$. Therefore, \begin{align*} A &= 2 \pi \bigl[\tfrac{1}{2} r^2 \bigr]^{r=R}_{r=0}; \\ or A &= 2 \pi \bigl[\tfrac{1}{2} R^2 - \tfrac{1}{2}(0)^2\bigr]; \\ whence \; A &= \pi R^2. \end{align*}

Another Exercise.

Let us find the mean ordinate of the positive part of the curve $y = x - x^2$, which is shown in Figure 60. To find the mean ordinate, we shall have to find the area of the piece $OMN$, and then divide it by the length of the base $ON$. But before we can find the area we must ascertain the length of the base, so as to know up to what limit we are to integrate. At $N$ the ordinate $y$ has zero value; therefore, we must look at the equation and see what value of $x$ will make $y = 0$. Now, clearly, if $x$ is $0$, $y$ will also be $0$, the curve passing through the origin $O$; but also, if $x=1$, $y=0$; so that $x=1$ gives us the position of the point $N$.

Then the area wanted is \begin{align*} &= \int^{x=1}_{x=0} (x-x^2)\, dx \\ &= \left[\tfrac{1}{2} x^2 - \tfrac{1}{3} x^3 \right]^{1}_{0} \\ &= \left[\tfrac{1}{2} - \tfrac{1}{3} \right] - [0-0] \\ &= \tfrac{1}{6}. \end{align*}

But the base length is $1$.

Therefore, the average ordinate of the curve $= \frac{1}{6}$.

[Note–It will be a pretty and simple exercise in maxima and minima to find by differentiation what is the height of the maximum ordinate. It must be greater than the average.]

The mean ordinate of any curve, over a range from $x= 0$ to $x = x_1$, is given by the expression, \[ \text{mean $y$} = \frac{1}{x_1} \int^{x=x_1}_{x=0} y · dx. \]

One can also find in the same way the surface area of a solid of revolution.

Example. The curve $y=x^2-5$ is revolving about the axis of $x$. Find the area of the surface generated by the curve between $x=0$ and $x=6$.

A point on the curve, the ordinate of which is $y$, describes a circumference of length $2\pi y$, and a narrow belt of the surface, of width $dx$, corresponding to this point, has for area $2\pi y\, dx$. The total area is \begin{align*} 2\pi \int^{x=6}_{x=0} y\, dx &= 2\pi \int^{x=6}_{x=0} (x^2-5)\, dx = 2\pi \left[\frac{x^3}{3} - 5x\right]^6_0 \\ &= 6.28 × 42=263.76. \end{align*}

Areas in Polar Coordinates.

When the equation of the boundary of an area is given as a function of the distance $r$ of a point of it from a fixed point $O$ (see Figure 61) called the pole, and of the angle which $r$ makes with the positive horizontal direction $OX$, the process just explained can be applied just as easily, with a small modification. Instead of a strip of area, we consider a small triangle $OAB$, the angle at $O$ being $d\theta$, and we find the sum of all the little triangles making up the required area.

The area of such a small triangle is approximately $\dfrac{AB}{2}×r$ or $\dfrac{r\, d\theta}{2}×r$; hence the portion of the area included between the curve and two positions of $r$ corresponding to the angles $\theta_1$ and $\theta_2$ is given by \[ \tfrac{1}{2} \int^{\theta=\theta_2}_{\theta=\theta_1} r^2\, d\theta. \]

A thin spherical shell has for volume $4\pi x^2\, dx$ (see Figure 59; summing up all the concentric shells %[xref, Page] which make up the sphere, we have \[ \text{volume sphere} = \int^{x=r}_{x=0} 4\pi x^2\, dx = 4\pi \left[\frac{x^3}{3} \right]^r_0 = \tfrac{4}{3} \pi r^3. \]

We can also proceed as follows: a slice of the sphere, of thickness $dx$, has for volume $\pi y^2\, dx$ (see Figure 62). Also $x$ and $y$ are related by the expression \[ y^2 = r^2 - x^2. \] \begin{align*} Hence \; \text{volume sphere} &= 2 \int^{x=r}_{x=0} \pi(r^2-x^2)\, dx \\ &= 2 \pi \left[ \int^{x=r}_{x=0} r^2\, dx - \int^{x=r}_{x=0} x^2\, dx \right] \\ &= 2 \pi \left[r^2x - \frac{x^3}{3} \right]^r_0 = \frac{4\pi}{3} r^3. \end{align*}

(2) Find the volume of the solid generated by the revolution of the curve $y^2=6x$ about the axis of $x$, between $x=0$ and $x=4$.

The volume of a strip of the solid is $\pi y^2\, dx$. \begin{align*} Hence \; \text{volume} &= \int^{x=4}_{x=0} \pi y^2\, dx = 6\pi \int^{x=4}_{x=0} x\, dx \\ &= 6\pi \left[ \frac{x^2}{2} \right]^4_0 = 48\pi = 150.8. \end{align*}

On Quadratic Means.

In certain branches of physics, particularly in the study of alternating electric currents, it is necessary to be able to calculate the quadratic mean of a variable quantity. By “quadratic mean” is denoted the square root of the mean of the squares of all the values between the limits considered. Other names for the quadratic mean of any quantity are its “virtual” value, or its “r.m.s.” (meaning root-mean-square) value. The French term is valeur efficace . If $y$ is the function under consideration, and the quadratic mean is to be taken between the limits of $x=0$ and $x=l$; then the quadratic mean is expressed as \[ \sqrt[2] {\frac{1}{l} \int^l_0 y^2\, dx}. \]

Examples (1) To find the quadratic mean of the function $y=ax$ (Figure 63).

Here the integral is $\int^l_0 a^2 x^2\, dx$, which is $\frac{1}{3} a^2 l^3$.

Dividing by $l$ and taking the square root, we have \[ \text{quadratic mean} = \frac{1}{\sqrt 3}\, al. \]

Here the arithmetical mean is $\frac{1}{2}al$; and the ratio of quadratic to arithmetical mean (this ratio is called the form-factor) is $\dfrac{2}{\sqrt 3}=1.155$.

(2) To find the quadratic mean of the function $y=x^a$.

The integral is $\int^{x=l}_{x=0} x^{2a}\, dx$, that is $\dfrac{l^{2a+1}}{2a+1}$. Hence quadratic mean = $\sqrt[2]{\dfrac{l^{2a}}{2a+1}}$.

(3) To find the quadratic mean of the function $y=a^{\frac{x}{2}}$.

The integral is $\int^{x=l}_{x=0} (a^{\frac{x}{2}})^2\, dx$, that is $\int^{x=l}_{x=0} a^x\, dx$, or $\left[ \frac{a^x}{\log_\epsilon a} \right]^{x=l}_{x=0}$, which is $\dfrac{a^l-1}{\log_\epsilon a}$.

Hence the quadratic mean is $\sqrt[2] {\dfrac{a^l - 1}{l \log_\epsilon a}}$.

Exercises XVIII

(5) Find the area included between the two branches of the curve $y=x^2 ± x^{\frac{5}{2}}$ from $x=0$ to $x=1$, also the area of the positive portion of the lower branch of the curve (see Figure 30.

(6) Find the volume of a cone of radius of base $r$, and of height $h$.

(7) Find the area of the curve $y=x^3-\log_\epsilon x$ between $x=0$ and $x=1$.

(8) Find the volume generated by the curve $y=\sqrt{1+x^2}$, as it revolves about the axis of $x$, between $x=0$ and $x=4$.

(9) Find the volume generated by a sine curve revolving about the axis of $x$. Find also the area of its surface.

(10) Find the area of the portion of the curve $xy=a$ included between $x=1$ and $x = a$. Find the mean ordinate between these limits.

(11) Show that the quadratic mean of the function $y=\sin x$, between the limits of $0$ and $\pi$ radians, is $\dfrac{\sqrt2}{2}$. Find also the arithmetical mean of the same function between the same limits; and show that the form-factor is $=1.11$.

(12) Find the arithmetical and quadratic means of the function $x^2+3x+2$, from $x=0$ to $x=3$.

(13) Find the quadratic mean and the arithmetical mean of the function $y=A_1 \sin x + A_1 \sin 3x$.

(14) A certain curve has the equation $y=3.42\epsilon^{0.21x}$. Find the area included between the curve and the axis of $x$, from the ordinate at $x=2$ to the ordinate at $x = 8$. Find also the height of the mean ordinate of the curve between these points.

(15) Show that the radius of a circle, the area of which is twice the area of a polar diagram, is equal to the quadratic mean of all the values of $r$ for that polar diagram.

(16) Find the volume generated by the curve $y=±\dfrac{x}{6}\sqrt{x(10-x)}$ rotating about the axis of $x$.

Answers

(1) $\text{Area} = 60$; $\text{mean ordinate} = 10$.

(2) $\text{Area} = \frac{2}{3}$ of $a × 2a \sqrt{a}$.

(3) $\text{Area} = 2$; $\text{mean ordinate} = \dfrac{2}{\pi} = 0.637$.

(4) $\text{Area} = 1.57$; $\text{mean ordinate} = 0.5$.

(5) $0.572$, $0.0476$.

(6) $\text{Volume} = \pi r^2 \dfrac{h}{3}$.

(7) $1.25$.

(8) $79.4$.

(9) $\text{Volume} = 4.9348$; $\text{area of surface} = 12.57$ (from $0$ to $\pi$).

(10) $a\log_\epsilon a$,   $\dfrac{a}{a - 1} \log_\epsilon a$.

(12) $\text{Arithmetical mean} = 9.5$; $\text{quadratic mean} = 10.85$.

(13) $\text{Quadratic mean} = \dfrac{1}{\sqrt{2}} \sqrt{A_1^2 + A_3^2}$; $\text{arithmetical mean} = 0$. The first involves a somewhat difficult integral, and may be stated thus: By definition the quadratic mean will be \[ \sqrt{\dfrac{1}{2\pi} \int_0^{2\pi} (A_1 \sin x + A_3 \sin 3x)^2\, dx}. \] Now the integration indicated by \[ \int (A_1^2 \sin^2 x + 2A_1 A_3 \sin x \sin 3x + A_3^2 \sin^2 3x)\, dx \] is more readily obtained if for $\sin^2 x$ we write \[ \dfrac{1 - \cos 2x}{2}. \] For $2\sin x \sin 3x$ we write $\cos 2x - \cos 4x$; and, for $\sin^2 3x$, \[ \dfrac{1 - \cos 6x}{2}. \] Making these substitutions, and integrating, we get (see here) \[ \dfrac{A_1^2}{2} \left( x - \dfrac{\sin 2x}{2} \right) + A_1 A_3 \left( \dfrac{\sin 2x}{2} - \dfrac{\sin 4x}{4} \right) + \dfrac{A_3^2}{2} \left( x - \dfrac{\sin 6x}{6} \right). \] At the lower limit the substitution of $0$ for $x$ causes all this to vanish, whilst at the upper limit the substitution of $2\pi$ for $x$ gives $A_1^2 \pi + A_3^2 \pi$. And hence the answer follows.

(14) Area is $62.6$ square units. Mean ordinate is $10.42$.

(16) $436.3$. (This solid is pear shaped.)