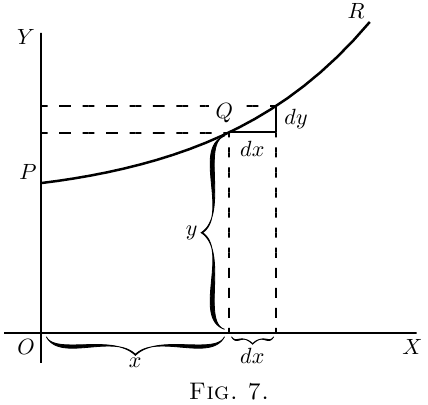
Let $PQR$, in Figure 7, be a portion of a curve plotted with respect to the axes of coordinates $OX$ and $OY$. Consider any point $Q$ on this curve, where the abscissa of the point is $x$ and its ordinate is $y$. Now observe how $y$ changes when $x$ is varied. If $x$ is made to increase by a small increment $dx$, to the right, it will be observed that $y$ also (in this particular curve) increases by a small increment $dy$ (because this particular curve happens to be an ascending curve). Then the ratio of $dy$ to $dx$ is a measure of the degree to which the curve is sloping up between the two points $Q$ and $T$. As a matter of fact, it can be seen on the figure that the curve between $Q$ and $T$ has many different slopes, so that we cannot very well speak of the slope of the curve between $Q$ and $T$. If, however, $Q$ and $T$ are so near each other that the small portion $QT$ of the curve is practically straight, then it is true to say that the ratio $\dfrac{dy}{dx}$ is the slope of the curve along $QT$. The straight line $QT$ produced on either side touches the curve along the portion $QT$ only, and if this portion is indefinitely small, the straight line will touch the curve at practically one point only, and be therefore a tangent to the curve.
This tangent to the curve has evidently the same slope as $QT$, so that $\dfrac{dy}{dx}$ is the slope of the tangent to the curve at the point $Q$ for which the value of $\dfrac{dy}{dx}$ is found.
We have seen that the short expression “the slope of a curve” has no precise meaning, because a curve has so many slopes–in fact, every small portion of a curve has a different slope. “The slope of a curve at a point” is, however, a perfectly defined thing; it is the slope of a very small portion of the curve situated just at that point; and we have seen that this is the same as “the slope of the tangent to the curve at that point.”
Observe that $dx$ is a short step to the right, and $dy$ the corresponding short step upwards. These steps must be considered as short as possible–in fact indefinitely short,–though in diagrams we have to represent them by bits that are not infinitesimally small, otherwise they could not be seen.
We shall hereafter make considerable use of this circumstance that $\dfrac{dy}{dx}$ represents the slope of the curve at any point.
If a curve is sloping up at $45°$ at a particular point,
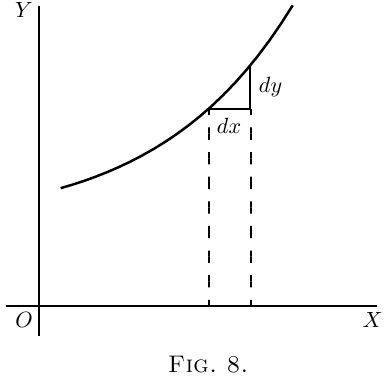
as in Figure 8, $dy$ and $dx$ will be equal, and the value
of $\dfrac{dy}{dx} = 1$.
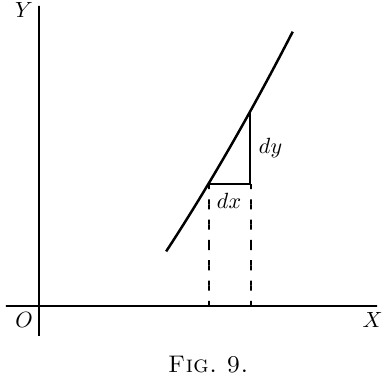
If the curve slopes up steeper than $45°$ (Figure 9),
$\dfrac{dy}{dx}$ will be greater than $1$.
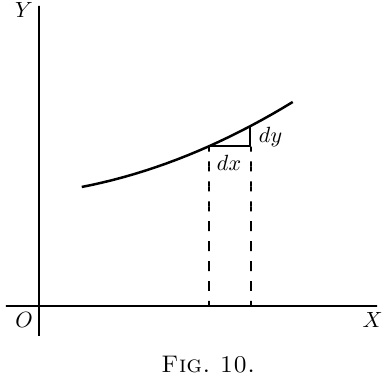
If the curve slopes up very gently, as in Figure 10,
$\dfrac{dy}{dx}$ will be a fraction smaller than $1$.
For a horizontal line, or a horizontal place in a
curve, $dy=0$, and therefore $\dfrac{dy}{dx}=0$.
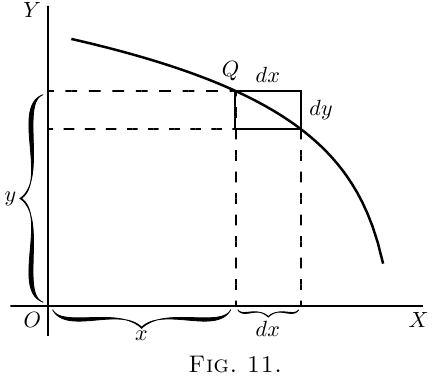
If a curve slopes downward, as in Figure 11, $dy$ will
be a step down, and must therefore be reckoned of
negative value; hence $\dfrac{dy}{dx}$ will have negative sign
also.
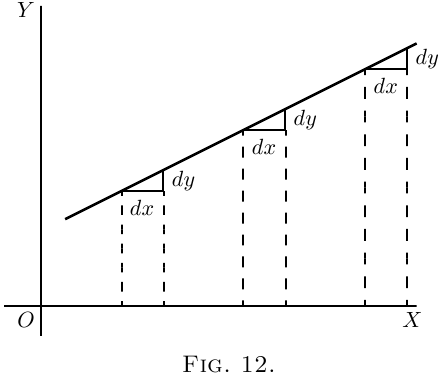
If the “curve” happens to be a straight line, like
that in Figure 12, the value of $\dfrac{dy}{dx}$ will be the same at
all points along it. In other words its slope is constant.
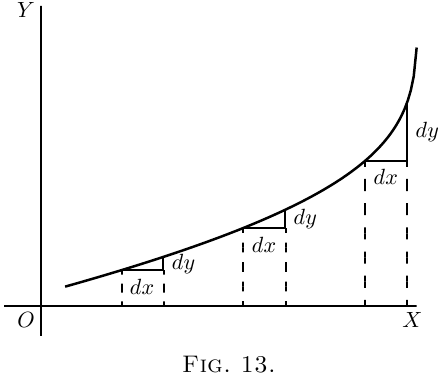
If a curve is one that turns more upwards as it
goes along to the right, the values of $\dfrac{dy}{dx}$ will become
greater and greater with the increasing steepness, as
in Figure 13.
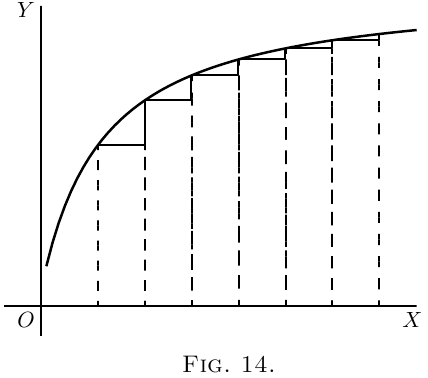
If a curve is one that gets flatter and flatter as it
goes along, the values of $\dfrac{dy}{dx}$ will become smaller and
smaller as the flatter part is reached, as in Figure 14.
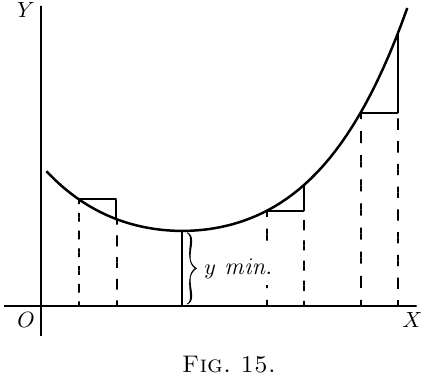
If a curve first descends, and then goes up again,
as in Figure 15, presenting a concavity upwards, then
clearly $\dfrac{dy}{dx}$ will first be negative, with diminishing
values as the curve flattens, then will be zero at the
point where the bottom of the trough of the curve is
reached; and from this point onward $\dfrac{dy}{dx}$ will have
positive values that go on increasing. In such a case
$y$ is said to pass by a minimum. The minimum
value of $y$ is not necessarily the smallest value of $y$,
it is that value of $y$ corresponding to the bottom of
the trough; for instance, in Figure 28 (the
value of $y$ corresponding to the bottom of the trough
is $1$, while $y$ takes elsewhere values which are smaller
than this. The characteristic of a minimum is that
$y$ must increase on either side of it.
Note–For the particular value of $x$ that makes
$y$ a minimum, the value of $\dfrac{dy}{dx} = 0$.
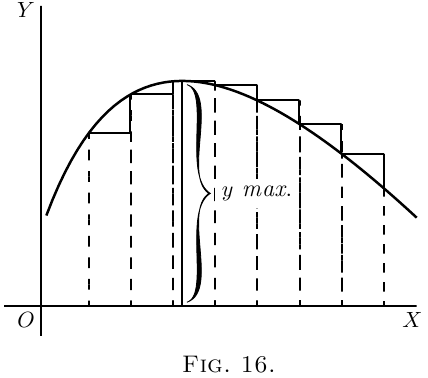
If a curve first ascends and then descends, the
values of $\dfrac{dy}{dx}$ will be positive at first; then zero, as
the summit is reached; then negative, as the curve
slopes downwards, as in Figure 16. In this case $y$ is
said to pass by a maximum, but the maximum
value of $y$ is not necessarily the greatest value of $y$.
In Figure 28, the maximum of $y$ is $2\frac{1}{3}$, but this is by no
means the greatest value $y$ can have at some other
point of the curve.
Note–For the particular value of $x$ that makes
$y$ a maximum, the value of $\dfrac{dy}{dx}= 0$.
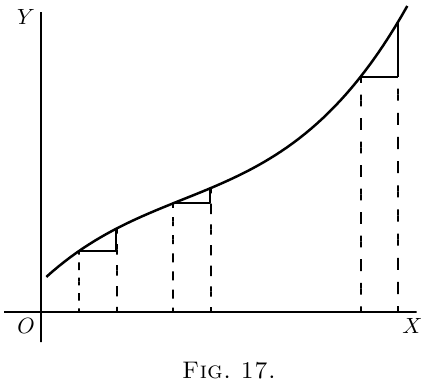
If a curve has the peculiar form of Figure 17, the
values of $\dfrac{dy}{dx}$ will always be positive; but there will
be one particular place where the slope is least steep,
where the value of $\dfrac{dy}{dx}$ will be a minimum; that is,
less than it is at any other part of the curve.
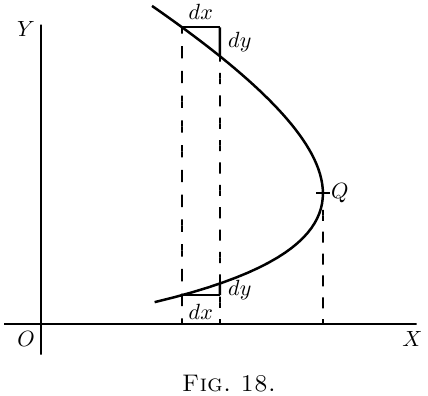
If a curve has the form of Figure 18, the value of $\dfrac{dy}{dx}$
will be negative in the upper part, and positive in the
lower part; while at the nose of the curve where it
becomes actually perpendicular, the value of $\dfrac{dy}{dx}$ will
be infinitely great.
Now that we understand that $\dfrac{dy}{dx}$ measures the
steepness of a curve at any point, let us turn to some
of the equations which we have already learned how
to differentiate.
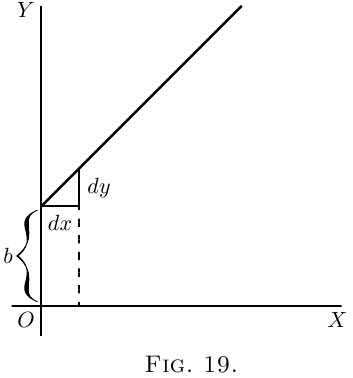
(1) As the simplest case take this:
\[
y=x+b.
\]
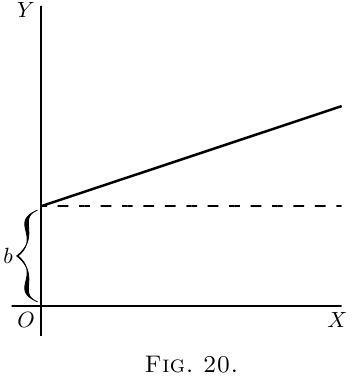
It is plotted out in Figure 19, using equal scales
for $x$ and $y$. If we put $x = 0$, then the corresponding
ordinate will be $y = b$; that is to say, the “curve”
crosses the $y$-axis at the height $b$. From here it
ascends at $45°$; for whatever values we give to $x$ to
the right, we have an equal $y$ to ascend. The line
has a gradient of $1$ in $1$.
Now differentiate $y = x+b$, by the rules we have
already learned (here and here), and we get $\dfrac{dy}{dx} = 1$.
The slope of the line is such that for every little
step $dx$ to the right, we go an equal little step $dy$
upward. And this slope is constant–always the
same slope.
(2) Take another case:
\[
y = ax+b.
\]
We know that this curve, like the preceding one, will
start from a height $b$ on the $y$-axis. But before we
draw the curve, let us find its slope by differentiating;
which gives $\dfrac{dy}{dx} = a$. The slope will be constant, at
an angle, the tangent of which is here called $a$. Let
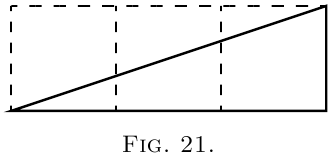
us assign to $a$ some numerical value–say $\frac{1}{3}$. Then we
must give it such a slope that it ascends $1$ in $3$; or
$dx$ will be $3$ times as great as $dy$; as magnified in
Figure 21. So, draw the line in Figure 20 at this slope.
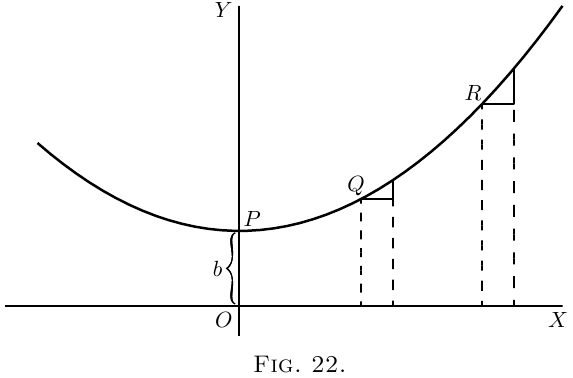
(3) Now for a slightly harder case.
\begin{align*}
Let
y= ax^2 + b.
\end{align*}
Again the curve will start on the $y$-axis at a height $b$
above the origin.
Now differentiate. [If you have forgotten, turn
back to here; or, rather, don't turn back, but think
out the differentiation.]
\[
\frac{dy}{dx} = 2ax.
\]
This shows that the steepness will not be constant:
it increases as $x$ increases. At the starting point $P$,
where $x = 0$, the curve (Figure 22) has no steepness–that
is, it is level. On the left of the origin, where
$x$ has negative values, $\dfrac{dy}{dx}$ will also have negative
values, or will descend from left to right, as in the
Figure.
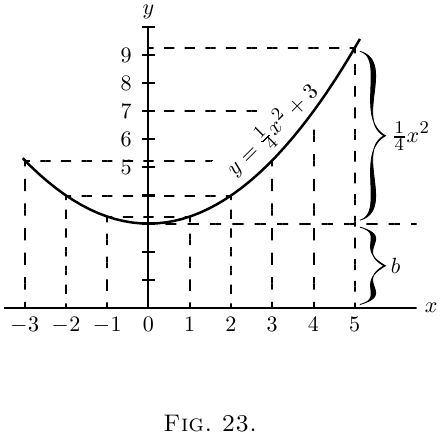
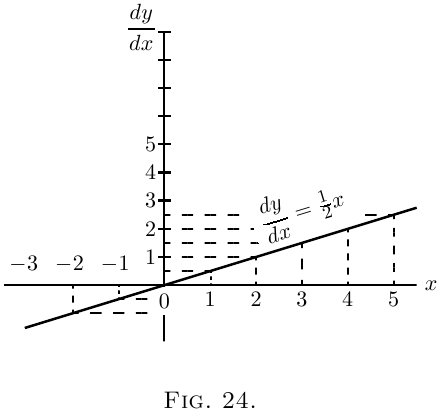
Let us illustrate this by working out a particular
instance. Taking the equation
\[
y = \tfrac{1}{4}x^2 + 3,
\]
and differentiating it, we get
\[
\dfrac{dy}{dx} = \tfrac{1}{2}x.
\]
Now assign a few successive values, say from $0$ to $5$,
to $x$; and calculate the corresponding values of $y$
by the first equation; and of $\dfrac{dy}{dx}$ from the second
equation. Tabulating results, we have: